Linear Elastic Fracture Mechanics with ANSYS APDL28 September 2022
ANSYS Parametric Design Language (APDL) is a powerful structured scripting language used to interact with the ANSYS Mechanical solver. Mechanical APDL (MAPDL), a finite element analysis program, is driven by APDL. APDL and MAPDL can be used for many tasks, ranging from creating geometries for analysis to setting up sophisticated solver settings for highly complex analyses. ANSYS was the first commercial simulation tool provider to offer users a versatile programming language to create parametric models for systemic analyses.
Cracks and flaws occur in many structures and components for several reasons. The material may be inherently defective. Cracks may be introduced during the manufacturing stage, or later as a result of environmental conditions. The presence of such cracks or flaws can significantly degrade the structural integrity of a component under the action of applied loads and environmental conditions.
In this article we are showing how to solve fracture mechanics problems using ANSYS APDL for linear elastic approach. It is advisable to start with a case for which an analytical solution exists. In this way, the designer can check if the numerical methodology (e.g. mesh size) is appropriate or not.
A crack is a high stress concentrator, so due to definition of material as linear elastic the stresses at the crack tip are very high (unrealistically) and cannot be used for assessment. A new parameter is used, which is called the Stress Intensity Factor (SIF).
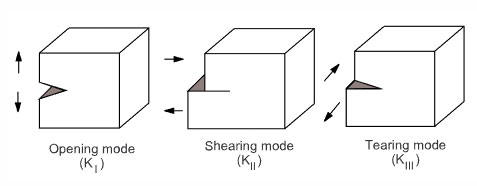
Depending on the failure kinematics (that is, the relative movement of the two surfaces of the crack), three fracture modes are distinguishable:
- Mode I - Opening or tensile mode
- Mode II - Shearing or sliding mode
- Mode III - Tearing or out-of-plane mode
Fracture is generally characterized by a combination of fracture modes.
We are using the reference solution for an arc-shaped specimen taken from the E 399-90 standard (Standard Test Method for Plane-Strain Fracture Toughness of Metallic Materials).
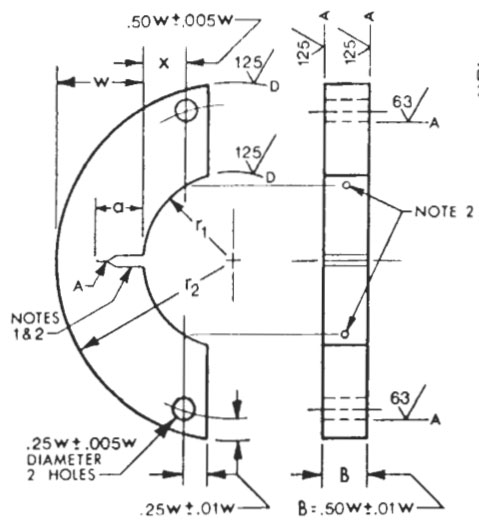
The dimensions of the arc-shaped specimen (picture from E 399-90 standard).
The standard provides an analytical relation for the computation of SIF. The specimen is loaded in tension, so we have only Mode I of crack opening.
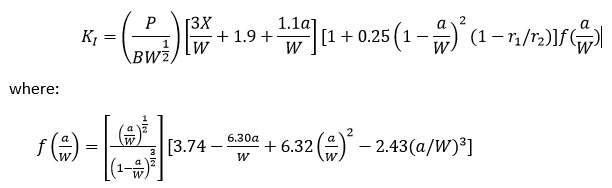
We have chosen r1 = 85 mm and r2 = 200 mm. The material is mild steel with a Young modulus of 2.1e5 N/mm2, a Poisson ratio of 0.3 and the expected fracture toughness of 50 MPa m1/2. The yield stress is assumed to be 350 MPa, so in accordance to E 399-90 standard, the minimum specimen thickness should be 51 mm to have plane strain condition; therefore we chose a thickness of 55 mm.
Modeling of the specimen
ANSYS APDL allows the use of scripting - scripts are, essentially, plain text files. In this case, it is recommendable to use this capability, instead of working interactively. The model is created using parameters, so just by changing the input parameter values, any variation can be easily generated. We performed the simulations for crack lengths varying from 25 to 55 mm, in steps of 5 mm. The load is the same for all cases and its magnitude is computed so that at the longest crack value (55 mm) the resulting SFI to be equal to the fracture toughness of the material. For the given dimensions of the specimen, a 65438 N force is required to obtain a stress intensity factor of 1580 MPa mm1/2 (or 50 MPa m1/2).
The specimen can be modeled using 2D element PLANE183 or SOLID186 in 3D. First, we show how the model is generated.
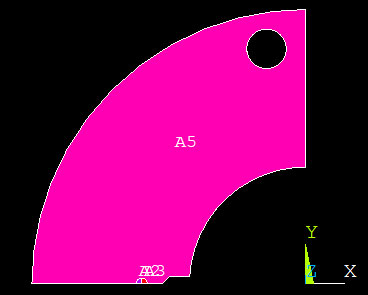
Only half of the specimen is modeled as we take advantage of the geometric and load symmetry. In order to capture the singularity from the crack tip it is necessary to use the command KSCON. To have a better control of the meshing, some circular subdivisions are created, centered on the crack tip.
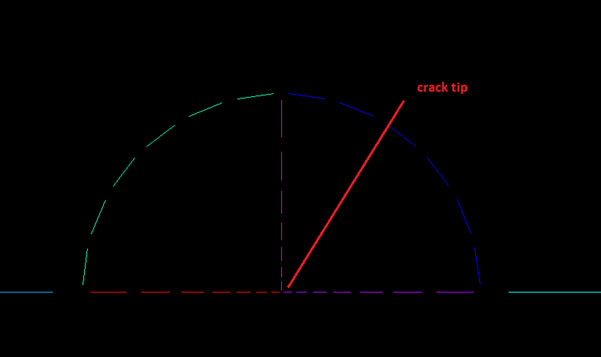
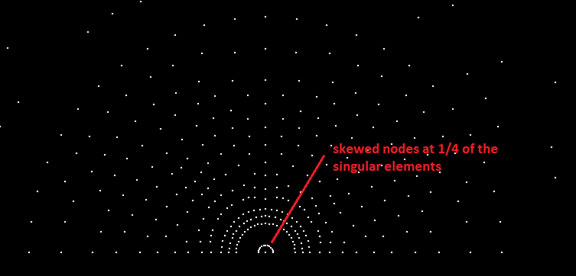
By controlling the number of line divisions on the circular regions radial edges, together with the KSCON command we can obtain a fine mesh with singular elements around the crack tip.

Mesh around crack tip

The applied boundary conditions
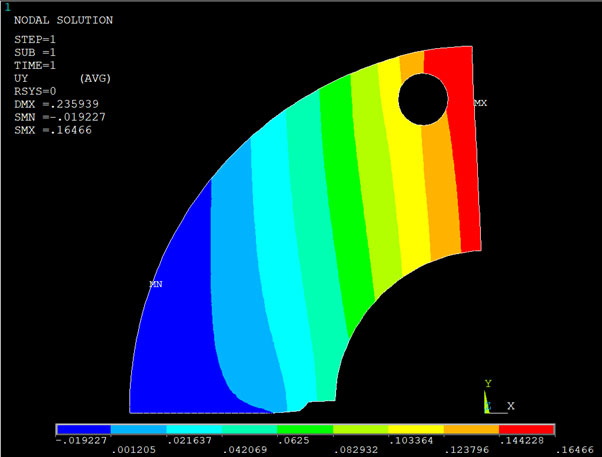
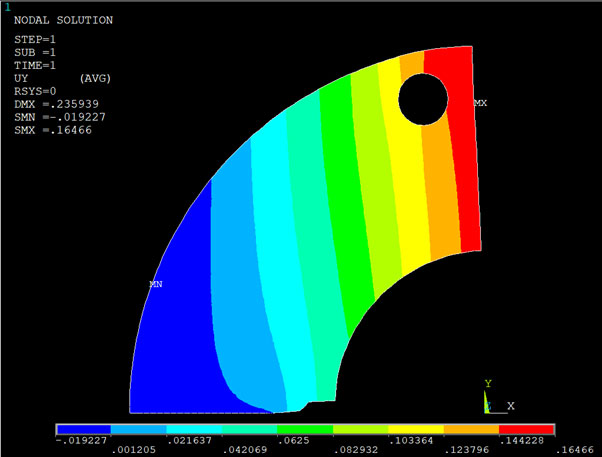
The displacements in vertical direction (mm) for 35 mm long crack (half 2D model).
By using the PRCINT command we can display the computed SFI for all the contours. We requested 6 contours. Theoretically, the SFI are independent of the contour. The values should be the same, but due to the fact it is a numerical method, some very small variations are observed. If the variations are very small, this is an indication that the mesh is sufficiently refined.

For this problem, we do not need the full model, but we included it for illustrative purposes. The easiest way is to make a mirror of geometry, together with the associated mesh, and merge the resulting coincident nodes on the symmetry line.
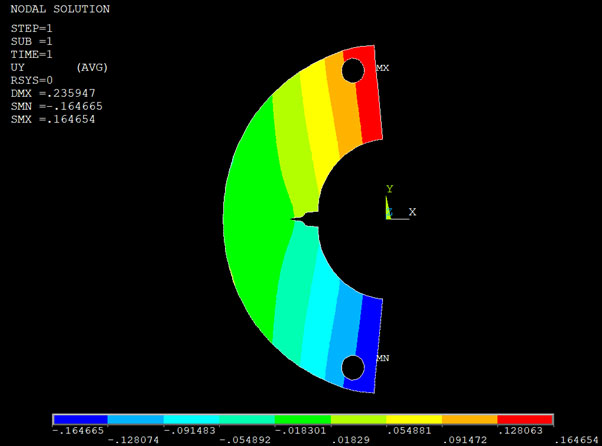
The displacements in vertical direction (mm) for 35 mm long crack (full 2D model).
We are now showing how to create the 3D model. One problem is that KSCON command is not available for 3D. However, the analysis can be performed even without singular elements around crack tip, provided they are small enough (in relation to the crack size). There is a possibility to have singular elements by using a modeling trick: the 2D geometry with the corresponding 2D mesh can be extruded and, thus, 3D singular elements are generated.

The half 3D model with applied boundary conditions (55 mm crack).
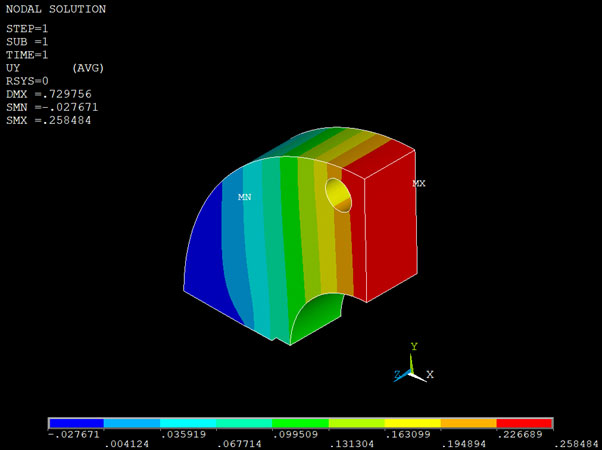
The displacements in vertical direction (mm) for 55 mm long crack (half 3D model).
After calculating the results with the 3D model, by using PRCINT command we can obtain the values of the SFI on the requested number of contours, for each node along the crack front.
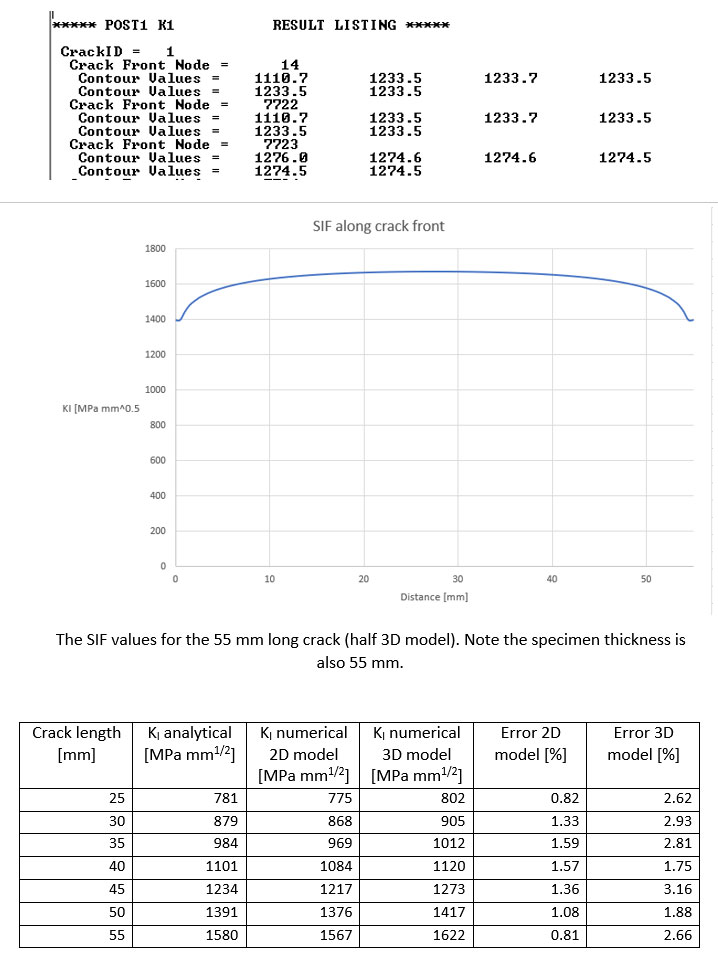
The usage of the scripts in ANSYS APDL is very productive, as new variants can be very easily and quickly generated. The following movie shows the efficiency of the script:
Conclusions
- ANSYS APDL provides very powerful features and tools to perform fracture mechanics calculations.
- For modeling procedure calibration and verification, it is recommended to start with an analytical case. We used singular elements of 0.5 mm at the crack tip. It is advisable to test the numerical convergence with at least two mesh densities.
- The correlation of the results is so good for 2D because the formulation of the PLANE183 element is plane strain, so it fits the theoretical formula very well. For the 3D model, the real end effects are evident, but nevertheless the correlation is still acceptable.
- For this geometry, the generation of 3D mesh with singular elements is quite easy because the crack front is a straight line. We will show in a future article how to generate such elements for a curved crack front.
- Scripting in ANSYS APDL may require some effort, but once completed, any possible variants can be generated very quickly with such script.
- We concentrated in this article on the computation of SFI (stress intensity factor). This is the most widely used parameter by designers. ANSYS offers the possibility to compute the following fracture mechanics parameters: J-Integral, Energy-Release Rate, Stress Intensity Factor, T-Stress, Material Force and C*-Integral.




